Soulja Boy Tweets Death Threat @ Gillie Da Kid

By
Jacky Jasper
-

gillie-kid-vs-soulja-boy

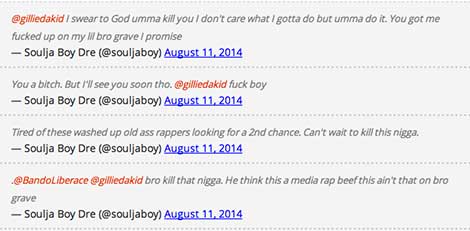
“Can’t wait to kill this nigga”

Soulja Boy appears to have taken the growing beef he’s got with Gillie to the next level. This, after Gillie demanded an apology from Soulja Boy for “not staying in his lane.” Soulja Boy has since dropped death threats. SMH..

“I’m gonna take off my Gucci belt and whoop his ass like the “kid” he is. -Soulja Boy

Peep the tweets:

souljaboy-tweets-death-threats

RELATED ARTICLESMORE FROM AUTHOR

29 COMMENTS

  1. He’s doing an awful lot of talking for someone who wouldn’t bust a grape in a fruit fight.

    These computer thugs absolutely slay me.. I guess when you snort up all your one hit wonder money, you have a lot of free time..

    • You right he ain’t gon bust a grape, nor is he gonna piss a hole in snow. All these feelings. These new ninjas are nothing more than vaginal secretions.

        • Yep you are right, that would work for him cause the heat from his coochie covering close to the snow would melt it then. Thanks WJJ, you solved that case.

    • I wouldn’t fight this nigga (souljah boy) cause i’m scared he might bleed on me….4 real tho

      • Oh yeah. He’s definitely an AIDS case . He and Lil Wayne. And Bow wow. Hell, most of them are a public health risk.. and every female they lay with too..

    • THIS THE FUNNIEST SHIT EVER RIGHT HERE!
      YOO CUZ A NIGGA JUST RAN TO POPO AND GOT THEM INVOLVED ON ME ,.. ITS LIKE YOU WAS THERE WHEN YOU TYPED THIS ! ,..I WAS GOING KNOCK HIS AZZ OUT COLD IN THA RAIN!

      • If he really wanted someone to be scared, he’d use one of my moves and be sitting on dudes couch in the dark when he comes home.. ALLEGEDLY! !! ALLEGEDLY! !

  3. This is very gay. I thought Souljah Boy would have been locked up by now. I guess he lied about going to prison to get street cred.

  4. He forgot Kat Stacks finished his career lmfao Men nowadays act worser than drag queens

    • Didn’t Kay Stacks find herself deported out of this country for some oddball reason?

  10. Does Soulja Boy need a storyline for “exploit ’em Mona’s show? Or is he trying to commit suicide by rap beef? He had better sit his scrawny ass down somewhere.

  11. Okay…Bet! No wishes of ill will but if dude is murked by Soulja’s hands or someone else, all I wanna see it the actual real live footage of Soulja Boy during his interrogation interview.

    Dumb ass. Doesn’t he know how social media has helped to gather suspects and criminals in solving or preventing actual crimes?

  12. Soulja is not a dude u hit with a closes fist.
    You must slap soulja boy like the bitch he is.
    I mean slap glitter from his hoe ass

  13. Souljah Boy is not worth a trip upstate with the chain-gang. Gillie The Kid could easily off skinny jeans and his crew… Why Not! In the streets, you threaten a brotha’s life, you better kill him on the spot. Otherwise, you’re a dead man walking. However, Souljah Boy is a pop star, he ain’t bout that life.

  14. My HSK family, mark my words…
    THIS is for certain to end badly one way or another. I know nothing about Gillie The Kid but he strikes me as an “old school type cat that does NOT play these kind of games.” Silly Boy, on the other hand is known for “flossin & frontin as if…” when in fact his daily life is nothing like he attempts to lead the world to believe via social media.

    Pray that Gillie does not get a hold to that boy EVER!!! It will be the end of 2 lives. GILLIE will be in prison & that “Boy” will be dead somewhere. Older cats like Gillie don’t take threats like that lightly (even via social media). The boy better ask somebody…

    • Boy u niggas r funny as hell. I’m still off that shit yall been committing on the funny ass beef. Real shit GDK a real stand up dude believe that

Comments are closed.